三角形と四角形
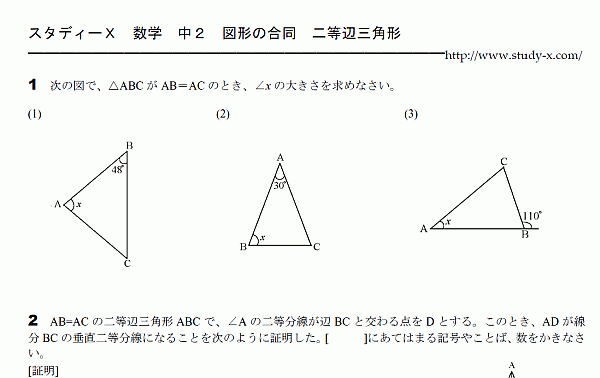
二等辺三角形
二等辺三角形について、 定義と、定理を学びます。 角度を出す問題もできなくてはなりません。
逆
仮定と結論を逆にすることを「逆」といいます。 逆が正しいとは限りません。
正三角形
正三角形についてのプリントです。 正三角形の定義と定理を使って、証明を進める問題です。
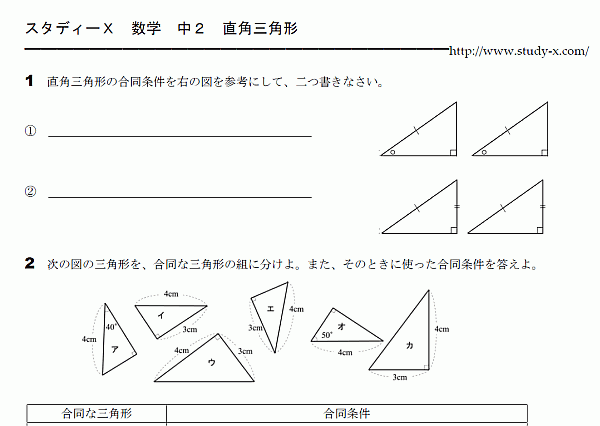
直角三角形の合同
直角三角形についてのプリントです。 直角三角形は、特別な合同条件を使うことができます。 斜辺と他の1辺がそれぞれ等しい。 斜辺とひとつの鋭角がそれぞれ等しい。 なぜ、上の二つの条件が成り立てば、合同と言えるのかもあわせて覚えておくべきです。
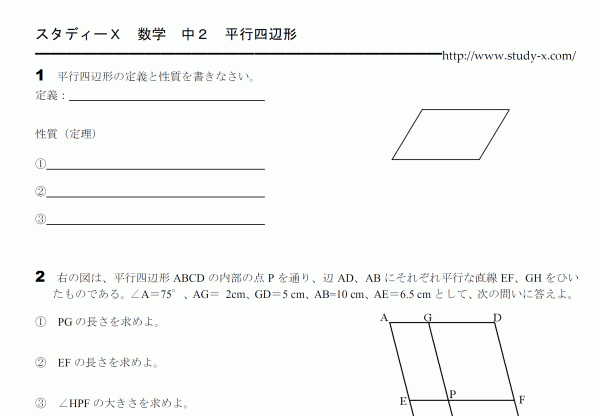
平行四辺形の性質
平行四辺形についてのプリントです。 小学生のときにもいくらか勉強しているようですが、それを言葉で定義します。 感覚的にも平行四辺形の性質をしっかり養っておきましょう。 3番の問題で平行線の錯角を見つけることができない生徒が多いです。 3番の問題は穴埋めとなっていますが、自分ですべての証明を書くことができるようになっている必要があります。
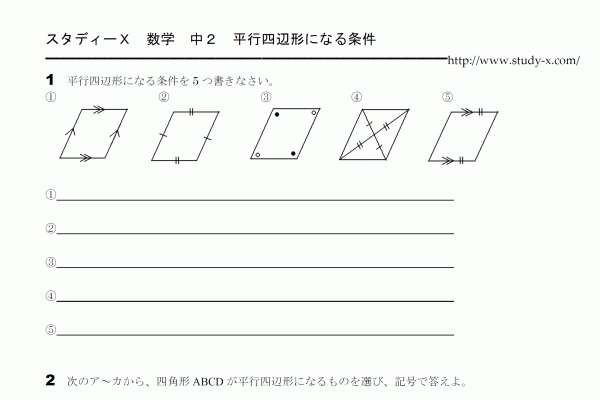
平行四辺形になる条件
平行四辺形になる条件についてのプリントです。
「2組の対辺がそれぞれ平行である」ということが分かれば平行四辺形であるといえます。
他にも
「2組の対辺がそれぞれ等しい」
「2組の対角がそれぞれ等しい」
「対角線がそれぞれの中点で交わる」
「1組の対辺が平行でその長さが等しい」
という条件がありますが、
なぜ、これらの条件が成り立てば
平行四辺形といえるのかをしっかりいえるようになっていて欲しいところです。
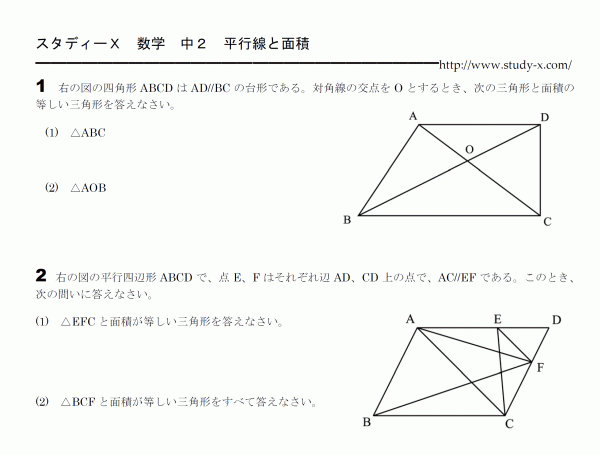
平行線と面積
平行線と面積のプリントです。
等積変形とも呼ばれるところです。
応用的な問題によく出題されますので、しっかり理解しておく必要があります。
まず、2つの三角形に共通な辺を見つけるとうまく行くことが多いです。
© 2022 study-x.com