1次関数
一次関数の基本
一次関数の基本の問題です。
中1のときに習った比例との違いに気をつけます。
文章を式にするのが苦手な生徒たちも多いです。
中1の「文字の式」を復習するとよいです。
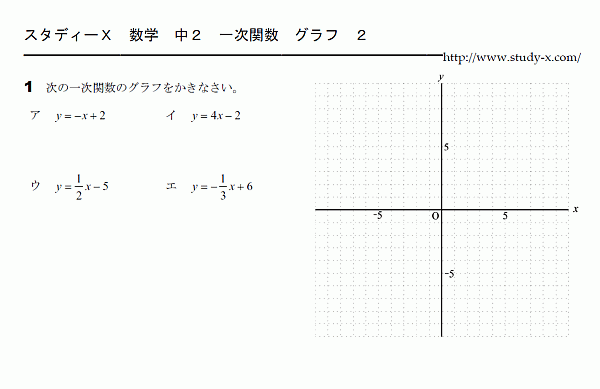
一次関数のグラフ
一次関数のグラフの問題です。 比例のグラフを平行移動させたもの、 と捉えるのが一番理解しやすいと思います。
一次関数のグラフ2
一次関数のグラフの問題のその2です。 まずは、切片をとり、 次に傾きからグラフをかきます。
一次関数の式とグラフ
一次関数の式とグラフが
どのように関連しているかを理解する問題です。
平行、右上がり、右下がり、などの言葉が
どういう意味なのかをしっかり考えてください。
一次関数の式とグラフ 切片が分数
一次関数のグラフの応用です。 切片が分数のときのグラフのかき方を練習します。 切片が分数のときは、 x座標、y座標がともに整数となるような点を探しだします。 表を書いて考えると分かりやすいかもしれません。 ともに整数となる点の座標が分かれば、 そこから傾きを利用して次の点をとります。
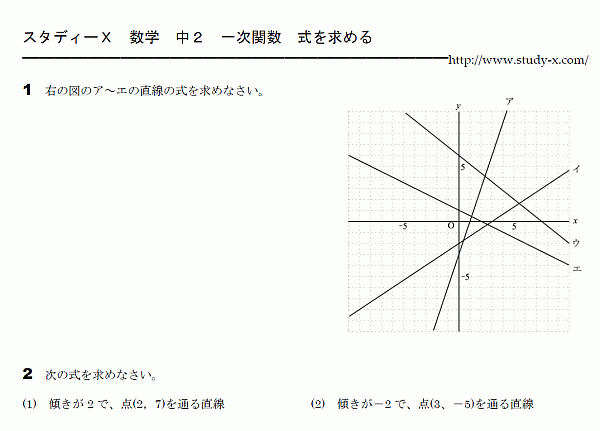
一次関数の式を求めること
一次関数のグラフを見て、 そこから式を求める問題です。 傾きと切片を調べることで、 式を完成させることができます。
一次関数の式を求めること2
一次関数の通る2点から、 一次関数の式を求める問題です。 やり方が2通りあります。 ひとつ目は傾きを求めてから、切片を求める方法。 ふたつ目はy = a x + b に2つの点を代入して、 2つの式を作り、 連立方程式で説く方法です。 どちらでもできるようにしてほしいですが、 ひとつ目のやり方のほうがグラフをイメージできて、 分かりやすいと思います。
変化の割合
変化の割合についてのプリントです。
変化の割合は、yの増加量を、xの増加量で割って求めることができます。
しかし、xの増加量とかyの増加量が何をあらわしているのかを
しっかり理解しないまま解いている生徒が多いです。
二元一次方程式とグラフ
二元一次方程式とグラフです。 二元一次方程式を変形することによって、 グラフに表すことができます。 その方法を練習します。
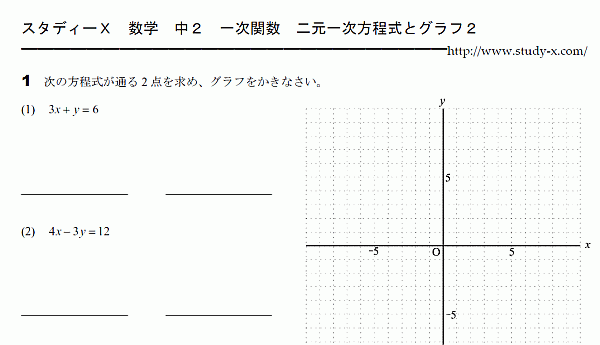
二元一次方程式とグラフ2
二元一次方程式とグラフのその2です。
グラフ上の2点を求めて、グラフを書きます。
x=0を代入して計算すると、y軸とどこで交わるかが分かります。
y=0を代入して計算すると、x軸とどこで交わるかが分かります。
その2点をもとに、グラフを書いていきます。
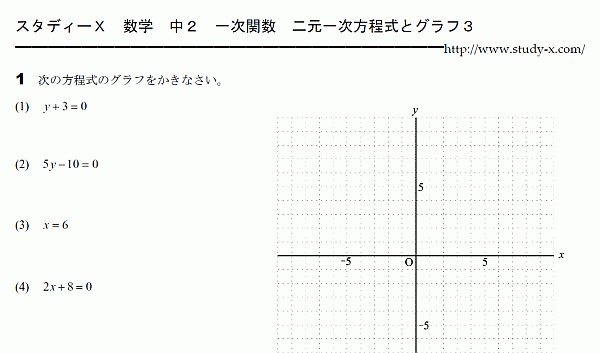
二元一次方程式とグラフ3
二元一次方程式とグラフのその3です。
y=~
x=~
のタイプの式のグラフをかきます。
y=~のグラフは、x軸に平行な直線になります。
x=~のグラフは、y軸に平行な直線になります。
連立方程式とグラフ
連立方程式とグラフです。 連立方程式の2つの式は、グラフに表すことができ、 2つの直線の交点と、連立方程式の解は一致します。
一次関数の利用 水そうの問題
一次関数の利用のうち、水そうの問題です。 実際の場面とグラフを結び付けて考えていきます。
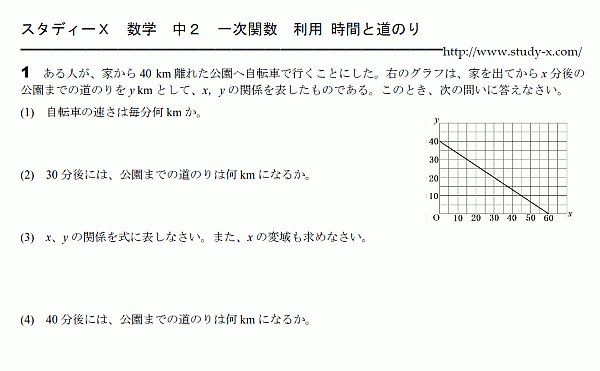
一次関数の利用 時間と道のり
一次関数の利用です。 時間と道のりに関する問題です。 時間と道のりのグラフは、 いつ、どの地点にいるのかが非常に分かりやすくなっています。 それを正確に読み取ります。
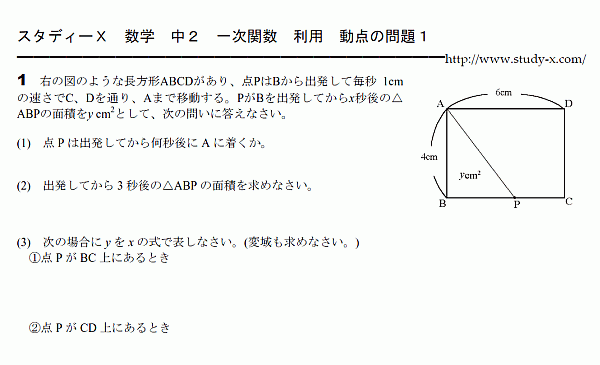
一次関数の利用 動点の問題
一次関数の利用です。 図形の上を点Pが移動する問題です。 動点の問題と呼ばれています。 入試問題で非常によく出題されるタイプの問題です。 それのうち、基本的なものです。
一次関数の利用 動点の問題2
一次関数の利用です。 図形の上を点Pが移動する問題の2枚目です。
© 2022 study-x.com