比例と反比例
一つの値が変わると、それにともなってもう一つの値が変わる。そのような関係をもつものは世の中にたくさんあります。
そのうち最も基本的なものが比例、そして反比例です。
式、表、グラフの3つで関連させて考えることができれば、理解できていると言えます。
座標や変域の考え方も、苦手な生徒が多いところです。初めからしっかり理解しておきたですね。
比例の基本1
比例の基本のプリントです。 ・ xの値を2倍、3倍・・・にするとそれにともなってyの値も2倍、3倍になる。 ・ y=ax (yはxに決まった数をかけて求めることが出来る) ・ aを比例定数という。 ・ yがxに比例するとき、比例定数はy÷xで求めることが出来る。 ・ x=1のときのyの値が比例定数である。
一方の値と他方の値の対応関係をしっかりつかみたいところです。
比例の基本2
比例の基本のプリントです。 この手の問題は非常によく出題されます。 文字の式のつくり方がわかっていれば大丈夫です。
比例するかどうか判断がつかない場合は、表をかいてみることをお勧めします。 x=1のときの計算、x=2のときの計算がすべて同じ形になるということを理解できます。 また表をかくことで、xが2倍、3倍になるとyが2倍、3倍になるかを確かめることも出来ます。
比例の式 変域
変域と比例の式を求める問題です。 1の変域の問題は、答え方が分からないかもしれません。 その意味でちょっと分かりづらい問題です。 でもぜひ意味を言えるようになって欲しいのです。
3のタイプの問題は、 私は「暗算で出せるものは積極的に暗算で出しなさい」と指導しています。 そのほうが比例の関係をつかみやすいし、 体になじませることができます。
代入して解くやり方も大事です。 しかし、安易にパターン化して覚えさせると、 比例の意味を考えなくなってしまいます。 それは避けなければなりません。
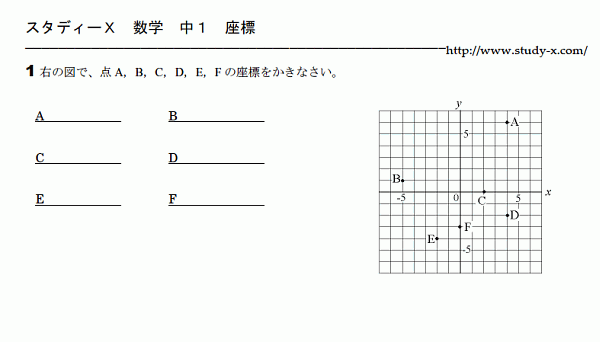
座標
座標はしくみが分かれば非常にやさしいところです。 反対にここがしっかり分かっていないと、 あとでグラフをかくときに非常に苦労します。
比例が苦手で・・・という生徒が 座標のしくみがよく分かっていなかったということが 何度もありました。 (x座標,y座標)の順に並んでいることを しっかり覚えて欲しいと思います。
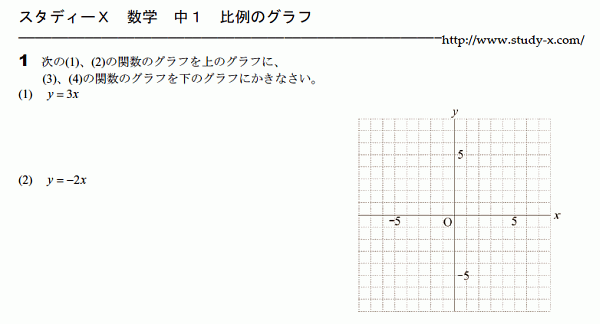
比例のグラフ
比例のグラフのプリントです。 簡単にかく方法もありますが、 最初のうちはまず表をかいて、 表をもとにしてグラフかくのが良いと思います。 そのうちに慣れてくると、 簡単なかき方を自分で法則化することができます。
反比例
反比例の基本のプリントです。 xとyの値をかけると一定になる、 というのがイメージをつかみやすいと思います。 式に書くときは一般に y=a/x となります。
反比例の式とグラフ
反比例の式とグラフのプリントです。 グラフは、まず表をかきます。 xとyがともに整数となる点をとり、 双曲線をかきます。
比例・反比例の利用
比例と反比例の利用のプリントです。 いわゆる応用問題です。 苦手な生徒が多くなります。 コツは、型に当てはめて解こうとするのではなく、 文章の状況をちゃんと想像して、 表をかいてみて考えることです。 そうすると、比例の関係なのか、 反比例の関係なのかが見えてきます。 この作業を繰り返して初めて、 すらすら解けるようになります。 3の(2)の問題は難問です。 表をかいて考えてみよう。
© 2022 study-x.com