平面図形
数字やグラフの問題が得意でも、図形はちょっと・・・という生徒が意外に多いです。
中には「図形は数学ではない」と豪語する生徒もいます。
図形の扱いが苦手でも慣れることで何とかなりますから、何度も練習して、図を描いて、理解していきましょう。
扇形の面積や弧の長さ中心角については、比例の考え方と同じなのですがなかなか分かりづらいようです。
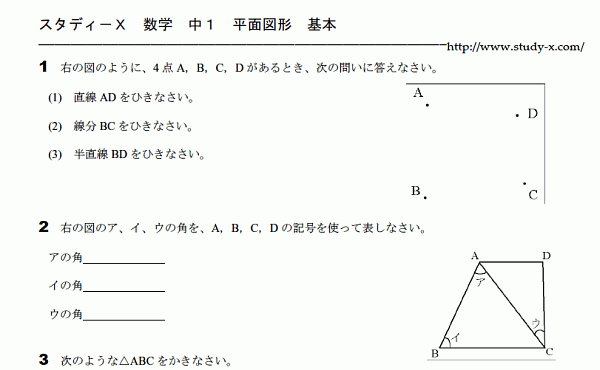
図形の基礎
お待たせいたしました。 リクエストの多かった、平面図形のプリントです。 最初は基本問題となります。 とくに、角の表し方をしっかり覚えていなくて、 わけがわからなくなる生徒が結構いますので、 注意して覚えてください。 用語をしっかり頭に入れておかないと、 解説の意味がわからなくなってしまいます。
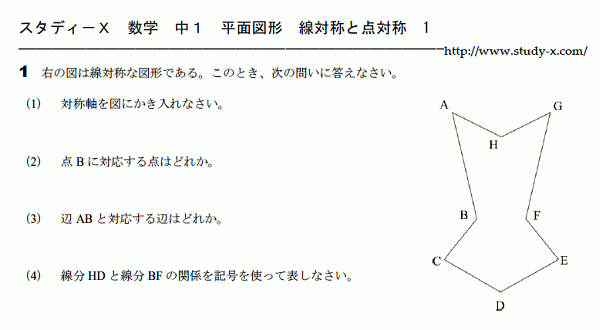
線対称と点対称
線対称と点対称のプリントです。 折ったときにぴったり重なる図形が線対称。 折り目を対称軸、または対称の軸といいます。
180度回転させたときにぴったり重なる図形が点対称です。 回転の中心となる点を対称の中心といいます。
図形が苦手な人へ。 ぜひ、実際に折ったり、回転させたりして確かめてください。 何度かやってみたら頭の中で折ったり回転させたりしてみることです。 繰り返すうちに、イメージできるようになってきます。
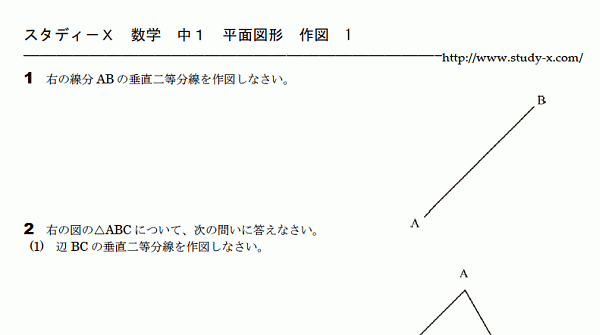
基本の作図
作図の問題です。 コンパスは距離を記憶する道具です。 1点からの距離が等しい点をたくさん集めると円になります。 2点からの距離が等しい点をたくさん集めると、2点を結ぶ線分の垂直二等分線となります。 2直線からの距離が等しい点をたくさん集めると、2直線が作る角の二等分線となります。 このことをしっかりイメージして作図していきましょう。
基本の作図2
作図の問題その2です。
おうぎ形の弧の長さと面積
扇形の弧の長さと面積を求める問題です。 まずは、中心角から、扇形が円に対してどのくらいの割合なのか(何倍なのか)を求める事が大事です。 公式を覚えて当てはめるだけの練習だと、あとあと意味がわからなくて苦労します。
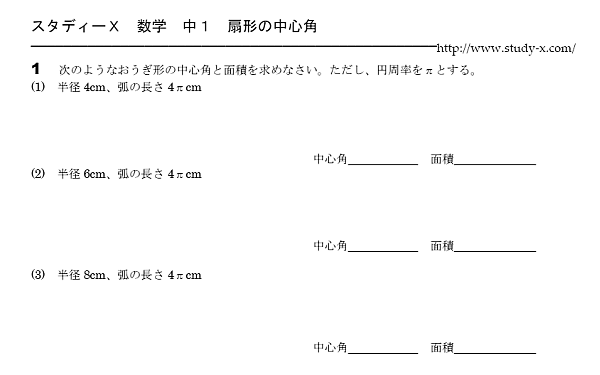
おうぎ形の中心角
扇形の中心角を求める問題です。 扇形の面積が分かっているときは、 円の面積と扇形の面積を比べて、扇形が何倍になっているのかを調べます。
扇形の弧の長さが分かっているときは、 円の周の長さと扇形の弧の長さを比べて、扇形が何倍になっているのかを調べます。
扇形の割合が分かったら、中心角を求めていきます。
© 2022 study-x.com