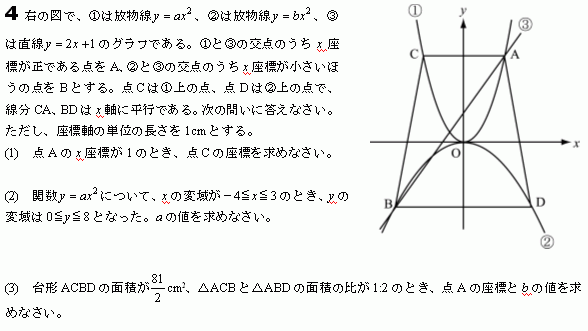
青森県2007年度 高校入試問題 第4問 です。
(3)の正解率はなんとAの座標が2.9%、bの値が1.7%。
これだけ正解率が低いと、入試本番では捨ててもいいですね。
この問題に時間をかけるより、他の問題やみなおしに時間を使ったほうが
有効でしょう。
しかし、本番以外ではどうやって解くのかを知っておくのは役に立ちます。
いろいろ考えてみよう。悩む価値はあります。
■ヒント
Aのx座標を t とおいて、方程式を作っていきます。
tはkでもいいし、pでもいいです。
媒介変数と呼ばれています。
■解説
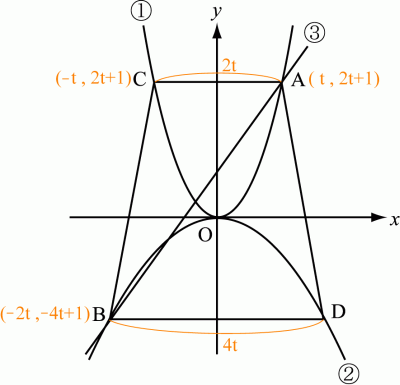
Aのx座標をtとすると、Aはy=2x+1上の点だから、
y=2t+1。
よって、A(t , 2t+1)。
AとCはy軸について、対称な点だから、
C(-t , 2t+1)。
よって、
AC=2t。
△ACBと△ABDの面積の比が1:2。
この二つの三角形はAC、BDをそれぞれの底辺だと考えると、
高さは等しい。
つまり、底辺の比が1:2となる。
だから、AC:BD=1:2。
AC=2tだから、BD=4t。
BD=4tということは、Bのx座標は4tの半分の2tにマイナスをつけたものとなる。
つまり、-2t。
Bは y=2x+1上の点だから、x座標に-2tを代入するとy=-4t+1。
よってB(-2t , -4t+1)。
すると、台形の高さは2t+1-(-4t+1)=6t。
よって、面積が81/2であることをもとにtの方程式をつくると、
(2t+4t)×6t÷2=81/2
これを解くと、t=±3/2。
Aのx座標はプラスだから、3/2。
A( 3/2 , 4 )
ここからbの値を求めます。
t=3/2なので、B(-2t , -4t+1)に代入すると、
B( -3 , -5)。
これをy=bx^2の式に代入して、
b=-5/9
◆登録カテゴリ
1000中学 数学 問題 | 1000中学 数学 問題 | 1100高校入試 数学 | 1250放物線と図形 | 12702次関数 媒介変数
