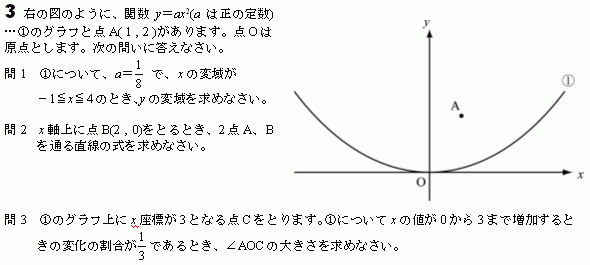
北海道2007年度高校入試問題の第3問です。
問3の難易度が高い(正答率19%)ので、解説を。
■ヒント
まず①の放物線のaの値を求めます。
次に点Cの座標を求めます。
△AOCがどんな三角形か調べます。
角度が与えられていないのに、
「角度を求めなさい」といわれています。
ということは、どこかに正三角形や三角定規の三角形など
特別な形があるはずです。
■解説
Cの座標は(3,1)となります。
この段階で、下のような図が浮かんでくると良いです。
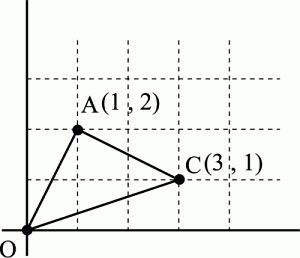
(まあ、ほとんどの生徒には浮かんできません。)
上の図を見て、
OA=ACで、角OAC=90°だから
直角二等辺三角形だな、と気がつければいいのですが、
これも大変です。
他にはOAとACとOCの長さを三平方の定理によって求めて、
比較してみてもいいです。
直角二等辺三角形であることに気がつきます。
いずれにせよ、「特別な形であるはずだ」と見当をつけて、
図形を眺めることが必要です。
◆登録カテゴリ
1000中学 数学 問題 | 1100高校入試 数学 | 1250放物線と図形
