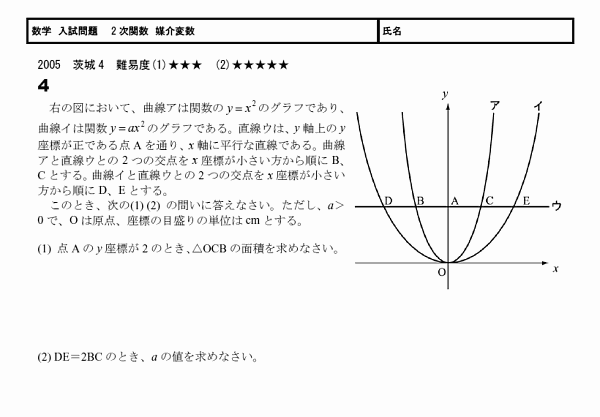
媒介変数を用いて解く問題です。
解説を書きましたが、
解き方の最後のほうがまだ習ってないという生徒も多いと思います。
ちょっと工夫すると、学習範囲内で解けるのですがねえ。
それともほかに簡単な解き方があるかもしれません。
見つけたときはお知らせください。
■09.01.29追記
アメリカ在住の石井様より、簡単な解き方をご紹介いただきました。
ありがとうございます。
以下に引用いたします。
==引用開始========
2005年の茨城県の4の(2)に
『簡単な解き方を見つけた方はお知らせください』とありましたのでコメントさせてください。
問題文を読む限りAのy座標は指定がなく、この問題文では『aの値が決まれば、DE:BCの比はAのy座標に関わらず一定である』というのは既知としても良いように感じられました。
もしそう考えれば単に、具体例を一つ取るだけでよいように思いました。
つまり、
C(1、1)の時を考えると、点Eは(2,1)になるはずなので、
a=1/4
とすぐに出してしまって構わないように感じました。
Cが(2、4)でも(3、9)でも同様になることを確認すれば、中学生でも確証が得られるのかなと。
少なくとも『aの値が決まれば、DE:BCの比はAのy座標に関わらず一定である』ことの証明を求められているわけでもないのですし、途中の式を要求されるわけでもないので、実践的にはこれで構わないように感じました。
あるいは変数をx座標にする形で、Cのx座標をsとして、
Sの2乗=a×{(2S)の2乗}
でSは0でないのでa=1/4と言うやり方だと学習範囲内になりましたでしょうか?
(ちょっと工夫すると、というのはこのやり方でしょうか?)
======引用ここまで
まったくおっしゃり通りです。
媒介変数もx座標に用いることで、計算を複雑にせずにすみます。
お恥ずかしながら、当時は気がつきませんでした。
HPに掲載の許可をお願いしましたら、
以下のお返事をいただきました。
==引用開始========
早速のお返事有難うございました。
私の解き方が参考になりましたら、うれしく思います。
いつも生徒に
『よく分からない時は簡単にして、具体的な例や簡単な例でどうなるかを考えよう。』
と言っています。
特に『整数の問題』や『規則性の問題』の時に役に立つ考えだと思いますが、
この問題についても、ある程度あてはまる部分があるかと感じた次第です。
具体的数値で考えて、規則性があることがみえれば、変数をたててみる考えにつながるようにいつも感じていま す。具体的例で考えた式がそのまま、変数を使った式をつくるヒントにもなるかと思います。
文章が拙くてお恥ずかしい限りですが、皆様のお役にたてるのでしたらメールをHPに載せていただくのは一向に構いません。
======引用ここまで
私も、「具体的な数字を入れて考えてみよう」と指導しています。
それなのに、気がつくことが出来ませんでした・・・・。
関数のときにもすぐに媒介変数に頼らずに、具体的な数字で考えてみるべきですね。
大変勉強になりました。
石井様ありがとうございました。
数学 高校入試問題 2次関数 媒介変数 05茨城4 難易度★★★★★(PDF)
全問題は2005年度 茨城県 高校入試問題 数学。
Tweet◆登録カテゴリ
1000中学 数学 問題 | 1100高校入試 数学 | 12702次関数 媒介変数
