いろいろな確率

いろいろな確率についてのプリントです。
くじをひく場合は、いつひいても同じ確率であること。
組み合わせは重複したものを除くこと。
これが一番理解しづらいポイントのようです。
いつ重複を削除すべきで、いつ削除すべきでないのかを理解するのが
ある生徒にとってはとても難しいようです。
確率の求めかた2

確率についてのプリントその2です。
樹形図や、表などを利用して、場合の数を求めていきます。
起こりうるすべての場合の数とその事象の数をできるだけ
わかりやすく整理するために樹形図や表を使います。
確率の求めかた

確率についてのプリントです。
確率のイメージは比較的みんな理解してくれますが、
次の単元になると・・・。
平行線と面積
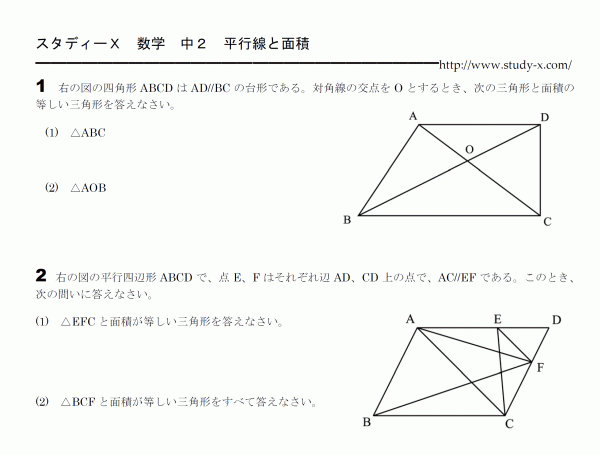
平行線と面積のプリントです。
等積変形とも呼ばれるところです。
応用的な問題によく出題されますので、しっかり理解しておく必要があります。
まず、2つの三角形に共通な辺を見つけるとうまく行くことが多いです。
平行四辺形になる条件
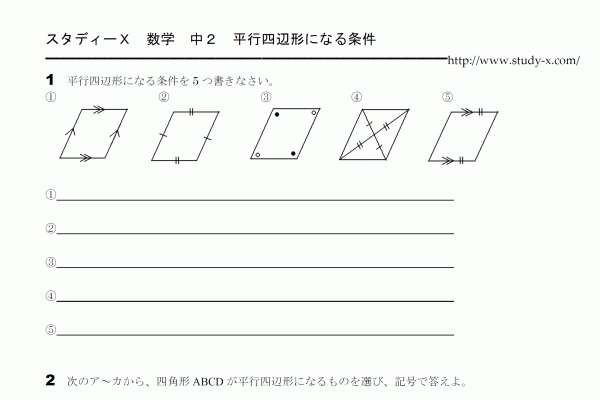
平行四辺形になる条件についてのプリントです。
「2組の対辺がそれぞれ平行である」ということが分かれば平行四辺形であるといえます。
他にも
「2組の対辺がそれぞれ等しい」
「2組の対角がそれぞれ等しい」
「対角線がそれぞれの中点で交わる」
「1組の対辺が平行でその長さが等しい」
という条件がありますが、
なぜ、これらの条件が成り立てば
平行四辺形といえるのかをしっかりいえるようになっていて欲しいところです。
平行四辺形
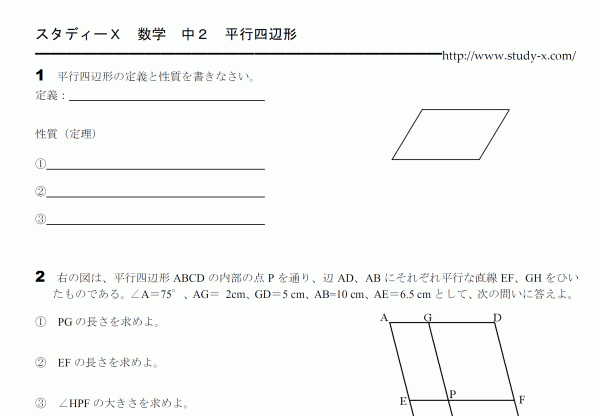
平行四辺形についてのプリントです。
小学生のときにもいくらか勉強しているようですが、それを言葉で定義します。
感覚的にも平行四辺形の性質をしっかり養っておきましょう。
3番の問題で平行線の錯角を見つけることができない生徒が多いです。
3番の問題は穴埋めとなっていますが、自分ですべての証明を書くことができるようになっている必要があります。
直角三角形
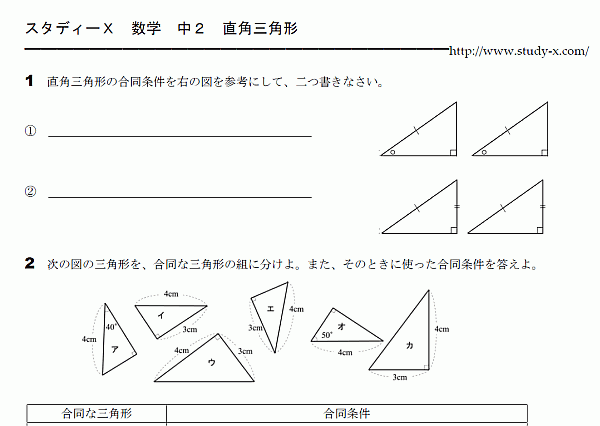
直角三角形についてのプリントです。
直角三角形は、特別な合同条件を使うことができます。
斜辺と他の1辺がそれぞれ等しい。
斜辺とひとつの鋭角がそれぞれ等しい。
なぜ、上の二つの条件が成り立てば、合同と言えるのかもあわせて覚えておくべきです。
正三角形

正三角形についてのプリントです。
正三角形の定義と定理を使って、証明を進める問題です。
逆

仮定と結論を逆にすることを「逆」といいます。
逆が正しいとは限りません。
二等辺三角形
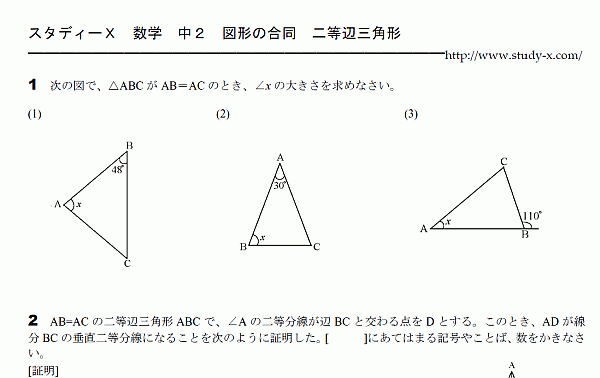
二等辺三角形について、
定義と、定理を学びます。
角度を出す問題もできなくてはなりません。
合同な三角形 証明 その2
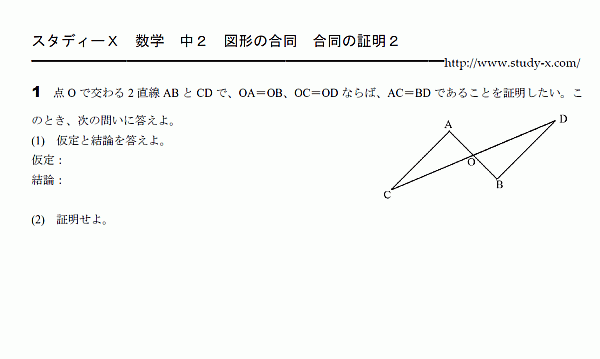
図形の問題です。
三角形の合同を証明する問題です。
すこし応用的な問題を含んでいます。
合同な三角形 証明
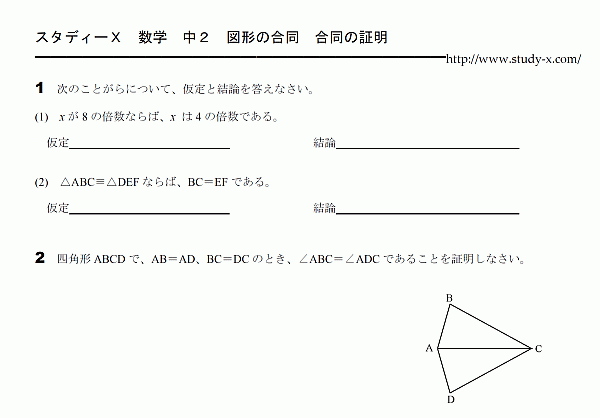
図形の問題です。
三角形の合同を証明する問題です。
穴埋め形式のものは、
対応する辺や角を書いて行くだけでできてしまいますので、
それだけで満足してはいけません。
自分で最初から最後まで
証明できるところまで頑張ってください。
合同な三角形 その2
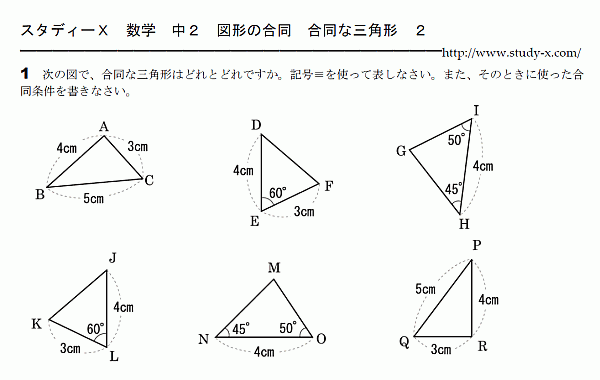
図形の問題です。
合同条件を正しく理解できているかを確かめる問題です。
合同な三角形
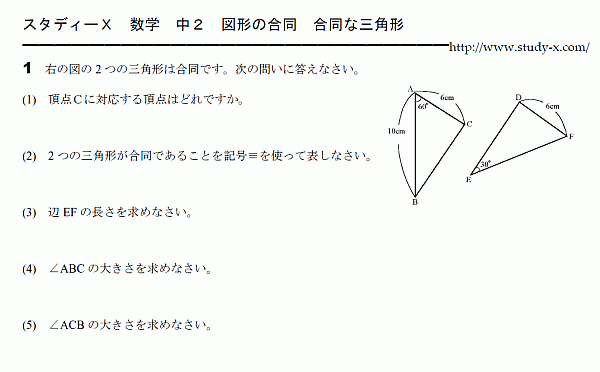
図形の問題です。
合同な三角形の問題です。
合同名三角形の性質と、
合同条件について復習するプリントです。
合同条件は必ず暗記しなければなりません。
その際、ただ暗記するのではなく、
「2辺」とはどの2辺なのか、
「その両端の角」とはどこの角なのか、
を意識しながら覚えることが大事です。
合同な三角形

図形の問題です。
合同な三角形の問題です。
合同名三角形の性質と、
合同条件について復習するプリントです。
合同条件は必ず暗記しなければなりません。
その際、ただ暗記するのではなく、
「2辺」とはどの2辺なのか、
「その両端の角」とはどこの角なのか、
を意識しながら覚えることが大事です。
多角形の角 応用
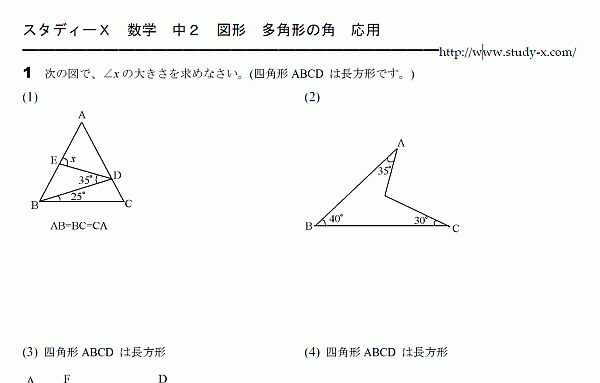
図形の問題です。
多角形の角の問題のうち、応用的な問題です。
苦手な生徒は、
計算して分かる角度をすべて書き込んでいくと、
答えまでたどり着くことができます。
多角形の角 外角

図形の問題です。
多角形の角の問題です。
外角の和が常に360度になることを利用して求めていきます。
多角形の角
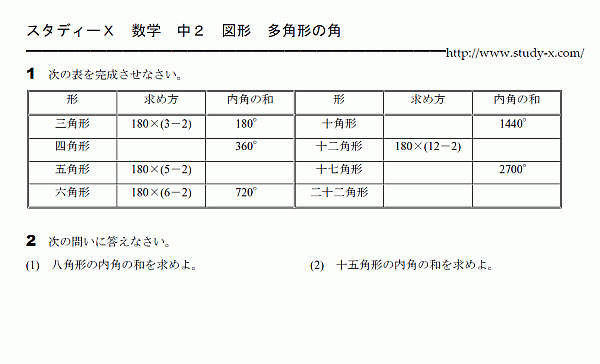
図形の問題です。
多角形の角の問題です。
多角形の角は、三角形に分割して考えます。
ある程度までは暗記するといいと思います。
三角形の角その2
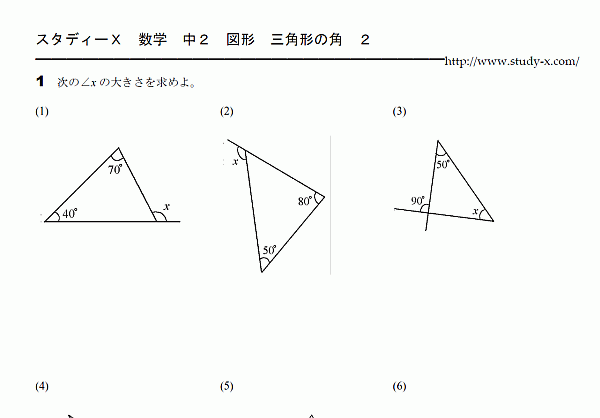
図形の問題です。
三角形の角についての問題です。
図形の問題は、苦手な生徒が多いので、
三角形についてもう一枚用意しました。
三角形の角
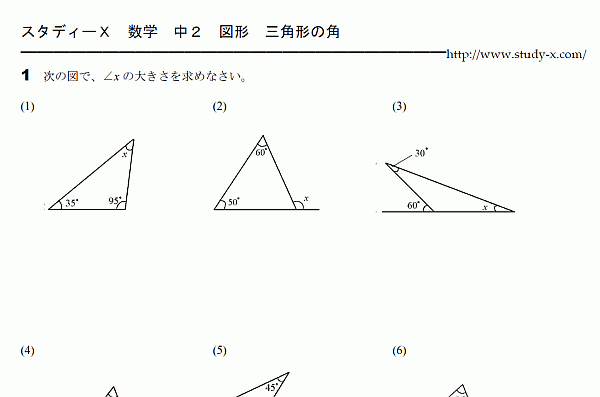
図形の問題です。
三角形の角についての問題です。
内角の和が180度になります。
1つの外角はそれと隣り合わない二つの内角の和に等しくなります。
二つ目は、結構重要です。
これをしっかり活用することで、計算の手間を減らし、
ミスを減らすことにつながります。
平行線と角
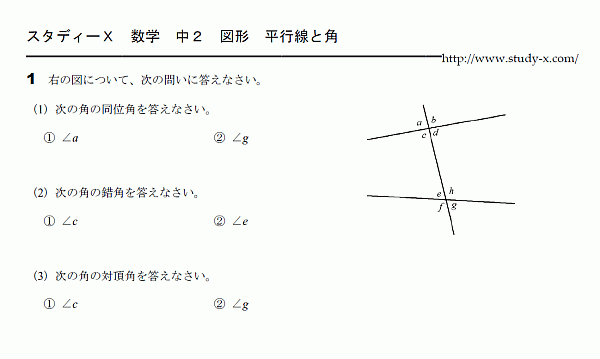
図形の問題です。
対頂角、錯角、同位角について学ぶプリントです。
平行線の錯角と同位角は等しくなります。
一次関数の利用 動点の問題 その2

一次関数の利用です。
図形の上を点Pが移動する問題の2枚目です。
一次関数の利用 動点の問題
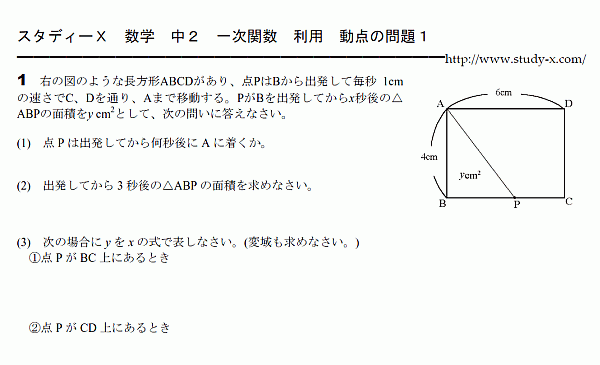
一次関数の利用です。
図形の上を点Pが移動する問題です。
動点の問題と呼ばれています。
入試問題で非常によく出題されるタイプの問題です。
それのうち、基本的なものです。
一次関数の利用 時間と道のり
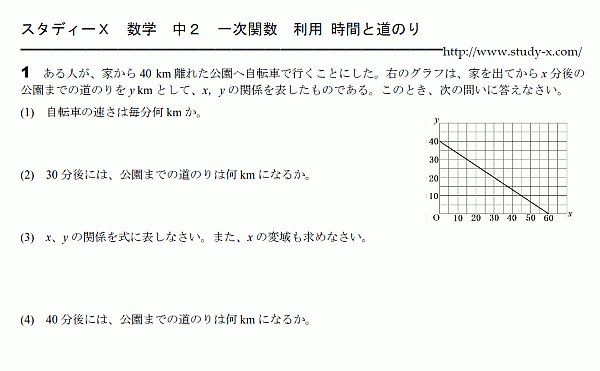
一次関数の利用です。
時間と道のりに関する問題です。
時間と道のりのグラフは、
いつ、どの地点にいるのかが非常に分かりやすくなっています。
それを正確に読み取ります。
一次関数のグラフの応用

一次関数のグラフの応用です。
切片が分数のときのグラフのかき方を練習します。
切片が分数のときは、
x座標、y座標がともに整数となるような点を探しだします。
表を書いて考えると分かりやすいかもしれません。
ともに整数となる点の座標が分かれば、
そこから傾きを利用して次の点をとります。
一次関数の利用 水そうの問題

一次関数の利用のうち、水そうの問題です。
実際の場面とグラフを結び付けて考えていきます。
連立方程式とグラフ

連立方程式とグラフです。
連立方程式の2つの式は、グラフに表すことができ、
2つの直線の交点と、連立方程式の解は一致します。
二元一次方程式とグラフ その3
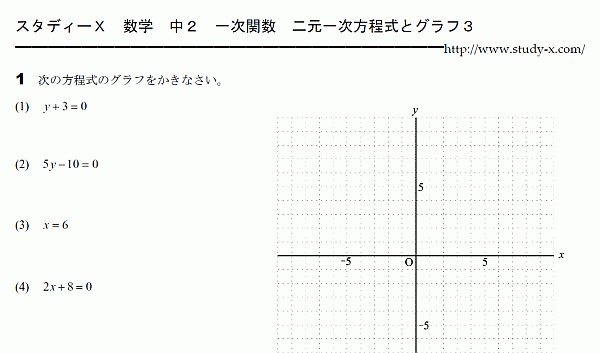
二元一次方程式とグラフのその3です。
y=〜
x=〜
のタイプの式のグラフをかきます。
y=〜のグラフは、x軸に平行な直線になります。
x=〜のグラフは、y軸に平行な直線になります。
二元一次方程式とグラフ その2
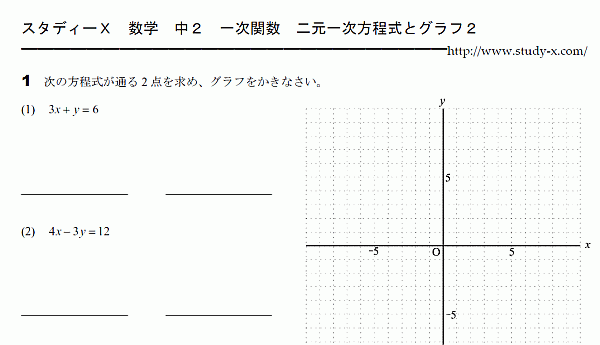
二元一次方程式とグラフのその2です。
グラフ上の2点を求めて、グラフを書きます。
x=0を代入して計算すると、y軸とどこで交わるかが分かります。
y=0を代入して計算すると、x軸とどこで交わるかが分かります。
その2点をもとに、グラフを書いていきます。
二元一次方程式とグラフ

二元一次方程式とグラフです。
二元一次方程式を変形することによって、
グラフに表すことができます。
その方法を練習します。
変化の割合

変化の割合についてのプリントです。
変化の割合は、yの増加量を、xの増加量で割って求めることができます。
しかし、xの増加量とかyの増加量が何をあらわしているのかを
しっかり理解しないまま解いている生徒が多いです。
一次関数の式を求める その2

一次関数の通る2点から、
一次関数の式を求める問題です。
やり方が2通りあります。
ひとつ目は傾きを求めてから、切片を求める方法。
ふたつ目はy = a x + b に2つの点を代入して、
2つの式を作り、
連立方程式で説く方法です。
どちらでもできるようにしてほしいですが、
ひとつ目のやり方のほうがグラフをイメージできて、
分かりやすいと思います。
一次関数の式を求める
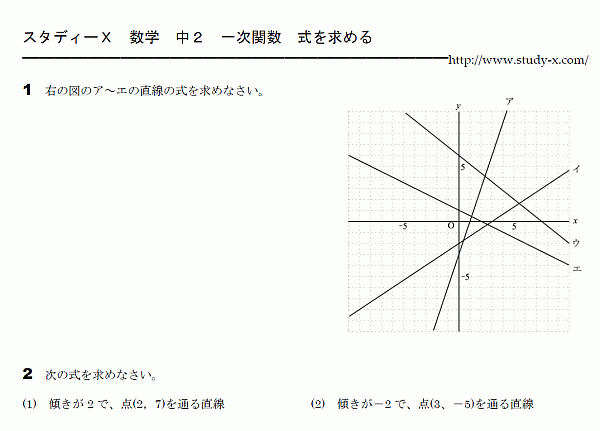
一次関数のグラフを見て、
そこから式を求める問題です。
傾きと切片を調べることで、
式を完成させることができます。
一次関数の式とグラフ

一次関数の式とグラフが
どのように関連しているかを理解する問題です。
平行、右上がり、右下がり、などの言葉が
どういう意味なのかをしっかり考えてください。
一次関数のグラフ その2
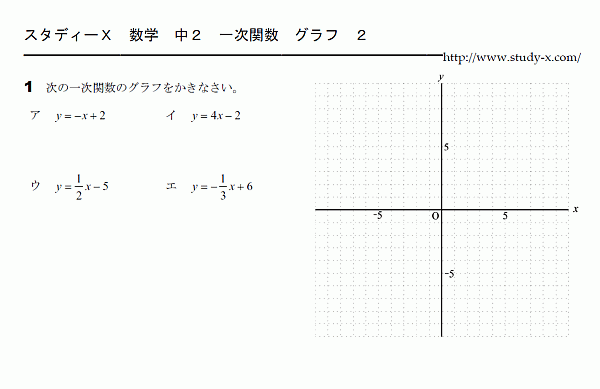
一次関数のグラフの問題のその2です。
まずは、切片をとり、
次に傾きからグラフをかきます。
一次関数のグラフ

一次関数のグラフの問題です。
比例のグラフを平行移動させたもの、
と捉えるのが一番理解しやすいと思います。
一次関数の基本

一次関数の基本の問題です。
中1のときに習った比例との違いに気をつけます。
文章を式にするのが苦手な生徒たちも多いです。
中1の「文字の式」を復習するとよいです。
連立方程式の利用 割合

連立方程式の利用です。
割合に関する問題です。
よくある食塩水の濃度の問題と、
昨年と今年の男女の人数の増減についての問題です。
連立方程式の利用 時間、距離、速さ

連立方程式の利用です。
時間、距離、速さに関する問題です。
「速さ」がどういうものであるのかを実感できているかどうかが鍵です。
連立方程式の利用 整数問題

連立方程式の利用です。
今回は、整数に関する問題です。
十の位の数をx、一の位の数をyとおいて、
整数を10x+yと表すのが基本となります。
十の位の数と一の位の数を入れ替えると、
10y+xとなります。
また各位の数の和はx+yです。
このあたりがすらすら出てくるようになっていてほしいところです。
連立方程式の利用 個数

連立方程式の利用です。
いわゆる文章題です。
個数や代金に関する問題です。
この手の問題が利用では一番やさしいものになります。
ここから先の難しいものにも理解をつなげていきましょう。
いろいろな連立方程式2

いろいろな連立方程式のその2です。
変数が4つあって、
そのうち2つが分かっているときの計算のやり方を学びます。
まあ、代入して計算するだけなのですが。
いろいろな連立方程式 かっこをふくむ

連立方程式のうち、ある程度式を整理してから、
加減法、代入法に持っていくものです。
式の計算の利用3

式の計算の利用のその3です。
式の計算の利用2

式の計算の利用のその2です。
覚えるべきパターンがいくつかあるので、
式の計算の利用は多めに用意してあります。
等式の変形

この単元は苦手な生徒が多いですね。
式がどういう意味を持っているのか、
よく考えるいい機会だと思います。
文字の式の利用1

文字の式の利用です。
整数の性質について、証明します。
最初はどういう流れで説明が進んでいるのか、理解できることが肝心です。
それから、自分でも説明が書けるように練習していきます。
文字の式 乗法と除法2

文字の式の乗法と除法の計算です。
乗法と除法が混ざっています。
ここは「マイナスを付け忘れる」といった符号のミスが目立つところです。
最後に答えがマイナスかプラスかを確認することです。
文字の式 乗法と除法1

文字の式の乗法と除法の計算です。
乗法だけの計算と、除法だけの計算に分かれています。
加法と減法3
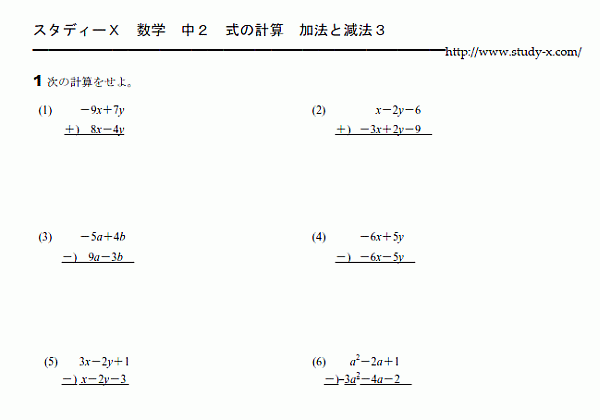
文字の式の加法と減法の練習です。
たての計算や、カッコつきの問題を練習します。
加法と減法3
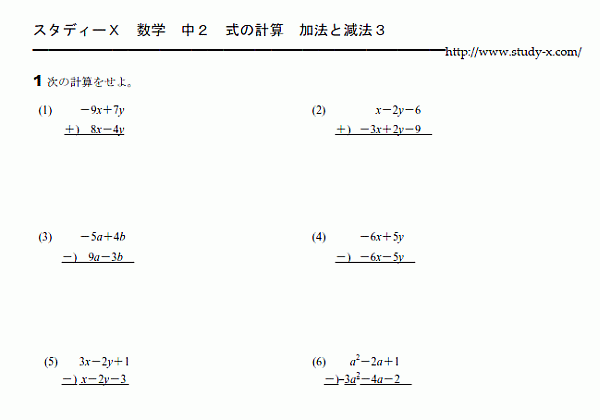
文字の式の加法と減法の練習です。
たての計算や、カッコつきの問題を練習します。
連立方程式 代入法

連立方程式のプリントです。
代入法です。
加減法と代入法を比べると、
ほとんどの生徒は加減法で解きます。
解きやすいのですかね。
代入法もなかなか捨てたものではありません。
しっかり練習しておきましょう。
連立方程式 加減法 係数が異なるもの

連立方程式のプリントです。
加減法のうち、係数の異なるものです。
方程式の両辺に同じ数をかけて、xかyの係数をそろえます。
どっちをそろえたほうがより数字が小さくてすむかをちゃんと考えてやってください。
計算ミスが減ります。
連立方程式 加減法 係数が異なるもの その1〜その10(PDF)
連立方程式 加減法 係数が同じもの

連立方程式のプリントです。
まずは加減法から。
xかyの係数があらかじめそろっているタイプの問題を6問ずつ10枚作成しました。
連立方程式は手順が複雑で長いです。
手順どおり機械的に解くのも必要ですが、
そればかりではいけません。
何のために何をしているのかを常に意識できているといいです。
中2 数学 式の計算 式の加法・減法

式の加法・減法の計算練習のプリントです。
このあとに習う、「連立方程式」へつながるところです。
中2 数学 式の計算 単項式と多項式

単項式と多項式の見分け問題。
項と係数の問題。
それと、同類項をまとめる問題が入っています。
同類項をまとめる問題は、
もうちょっと拡充する予定です。
